torch.nn简介#
pytorch提供了很多设计良好的模块来帮助构建和训练神经网络。为了充分利用它们的能力并为自己的问题定制神经网络,需要了解它们都在做什么,其中被用于构建神经网络 的torch.nn 模块就是我们要重点了解的。之前说到autograd可以实现反向传播功能, 但是如果直接用它来写神经网络的代码还是稍显复杂,而torch.nn 是专门为神经网络设计的模块化接口,它构建于 autograd 之上, 可用来定义和运行神经网络,使用它构建神经网络就会很简单。关于torch.nn的详细介绍,推荐大家查看官方文档介绍:WHAT IS TORCH.NN REALLY?,这里我们从简介绍。
1 以一个线性层为例简单说明#
我们知道神经网络典型的一层是一个线性组合加一个非线性激活函数。以线性组合为例,如果我们需要自己手写,那么就会像下面这样
import math
import torch
import numpy as np
# nn_sample是一个简单的示例数据文件
x_train = torch.Tensor(np.load("../data/nn_sample.npy"))
weights = torch.randn(784, 10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)
def linear(x):
return x @ weights + bias
preds = linear(x_train)
preds[0]
tensor([ 0.6236, -0.3339, -0.1948, 0.2624, -0.0028, -0.1041, -0.0390, 0.2814,
-0.0178, -0.0691], grad_fn=<SelectBackward0>)
假如样本真实输出都是1:
y_train = torch.ones(preds.shape)
我们定义loss函数是:
def loss_func(p, o):
return torch.mean((p - o) ** 2)
然后我们训练这一层线性层的时候就需要计算损失并反向传播,然后更新权值。
lr = 0.5
loss = loss_func(preds, y_train)
loss.backward()
with torch.no_grad():
weights -= weights.grad * lr
bias -= bias.grad * lr
weights.grad.zero_()
bias.grad.zero_()
如果我们使用nn中准备好的工具,那么整个过程就会变得更加清晰简洁。
class Linear(nn.Module):
def __init__(self):
super().__init__()
self.lin = nn.Linear(784, 10)
def forward(self, xb):
return self.lin(xb)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[10], line 1
----> 1 class Linear(nn.Module):
2 def __init__(self):
3 super().__init__()
NameError: name 'nn' is not defined
其中,nn.Linear是这样的:
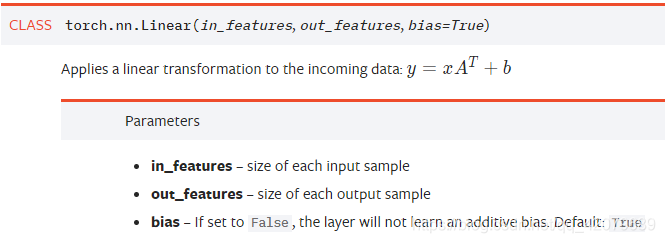
in_features指的是输入的二维张量的大小,即输入的 [batch_size, size] 中的size(输入图片的特征共有多少个,上一个全连接层神经元的个数)。
out_features指的是输出的二维张量的大小,即输出的二维张量的形状为[batch_size,output_size],当然,它也代表了该全连接层的神经元个数。
Linear其实就是对输入 Xn×i执行了一个线性变换,即:Yn×o = Xn×iWi×o + b ,其中W是模型要学习的参数,W的维度为 W i×o,b是o维的向量偏置,n为输入向量的行数(例如,你想一次输入10个样本,即batch_size为10,则n = 10 ),i为输入神经元的个数(例如你的样本特征数为5,则i = 5),o为输出神经元的个数。
从输入输出的张量的shape角度来理解,相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。
model = Linear()
loss = loss_func(model(x_train), y_train)
loss.backward()
with torch.no_grad():
for p in model.parameters():
p -= p.grad * lr
model.zero_grad()
事实上,loss_func在nn模块中都有现成的工具,整个过程会更简单,另外,梯度下降的优化算法也有专门的optim包来帮助实现,这些内容在最后一个实例中我们都会看到。总之,用nn等模块会更方便,接下来我们进一步看看最关键的神经网络通过nn包是如何构建的。
2 nn.Module类的使用#
torch.nn.Module类是所有神经网络模块(modules)的基类,我们用Pytorch写神经网络模型应该继承这个类,并重载__init__和forward函数。
把网络中具有可学习参数的层(如全连接层、卷积层等)放在构造函数 __init__()中;
不具有可学习参数的层(如ReLU、dropout、BatchNormanation层)最好也放在构造函数 __init__()中,如果不放在构造函数__init__里面,则在forward方法里面使用nn.functional来代替
forward方法是必须要重写的,它来具体实现各个层之间的连接。
下面来看一个两个非线性层的简单例子:
import torch
class Mlp(torch.nn.Module):
def __init__(self):
super(Mlp, self).__init__() # 调用父类的构造函数
self.lin1 = torch.nn.Linear(784, 256)
self.relu = torch.nn.ReLU()
self.lin2 = torch.nn.Linear(256, 10)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.lin1(x)
x = self.relu(x)
x = self.lin2(x)
x = self.sigmoid(x)
return x
model = Mlp()
model
Mlp(
(lin1): Linear(in_features=784, out_features=256, bias=True)
(relu): ReLU()
(lin2): Linear(in_features=256, out_features=10, bias=True)
(sigmoid): Sigmoid()
)
我们稍作解释,因为前面Python基础的地方我们没有涉及类的概念,所以这里我们从类开始说起。
类可以简单理解为一系列变量和方法的集合体,比如人物,我们要用代码虚拟化它,需要他/她的各种自然属性和社会属性以及行为,这些都可以用变量和函数来表达,这个集合体就是人这个类,当给这一系列属性赋予确定值时,我们就称之为实例化,这个实例化的产物就称作对象。
一个类可以被另一个类继承,例如中国人类继承人类,人这个类的内容中国人类都有,但是还可以包括其他专属于我国的特点。在python中,继承的形式就是上面示例的形式:
class Sonclass(ParentClass):
def __init__(self):
...
那么nn.Module就是Pytorch写好的一个类,我们写的类就继承了它的各类属性、方法,如果父类中一个函数被继承后,子类修改了其内容,那么子类的内容就会覆盖掉父类的,我们正是通过重写构造函数 __init__()和forward函数来实现神经网络的定制。在前者中,我们把神经网络的各层表达出来,在后者中,我们使用各层去作运算,连接在前者中构建的各层。
上面提到的“不具有可学习参数的层(如ReLU、dropout、BatchNormanation层)如果不放在构造函数__init__里面,则在forward方法里面使用nn.functional来代替”的意思是:如果ReLU等不在构造函数中标出,那么在forward里直接用同等作用的函数直接执行运算即可。
import torch
import torch.nn.functional as F
class Mlp(torch.nn.Module):
def __init__(self):
super(Mlp, self).__init__() # 调用父类的构造函数
self.lin1 = torch.nn.Linear(784, 256)
self.lin2 = torch.nn.Linear(256, 10)
def forward(self, x):
x = self.lin1(x)
x = F.relu(x)
x = self.lin2(x)
x = F.sigmoid(x)
return x
model = Mlp()
model
Mlp(
(lin1): Linear(in_features=784, out_features=256, bias=True)
(lin2): Linear(in_features=256, out_features=10, bias=True)
)
两种写法是一样的,关于nn.funtional和nn.Module的区别,大家可以自己去查一查。个人理解,就是没有可学习参数的,可能没区别,有可学习参数的前者不自带神经网络参数,后者则是有参数的。
